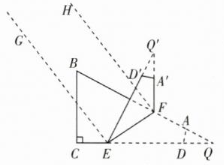
解:$(3)$如图,延长$BA,$$CD$交于点$Q,$延长$ED,$
$FA'$交于点$Q,$则对折后$\triangle EFQ $与$\triangle EFQ'$重合。
$ $由$(2)$的结论可得$2∠Q = ∠D'EC-∠A'FB,$
而$∠D'EC = 115°,$$∠A'FB = 45°,$
∴$2∠Q=115°-45°=70°,$则$∠Q = 35°。$
∵$∠C = 90°,$
∴$∠ABC=90°-35°=55°。$
$ (4)EG// FH,$不会改变。
理由如下:
如图,$EG $平分$∠D'EC,$$FH$平分$∠A'FB,$
∴$∠D'EG=∠CEG=\frac {1}{2}∠D'EC,$
$∠A'FH=∠BFH=\frac {1}{2}∠A'FB。$
$ $由对折可得$∠Q'EF=∠QEF,$$∠Q'FE=∠QFE,$
由$(2)$的结论可得$∠D'EC-∠A'FB = 2∠Q,$
即$∠D'EC=∠A'FB + 2∠Q。$
∴$∠D'EG=∠A'FH+∠Q,$
则$∠D'EG+∠D'EF+∠BFE+∠BFH=∠A'FH$
$+∠Q+∠QEF+∠BFH+∠BFE。$
∴$∠FEG+∠HFE=∠Q+∠QEF+∠Q'FE,$
又∵$∠Q+∠QEF+∠QFE = 180°,$
∴$∠FEG+∠HFE = 180°,$
∴$EG// FH。$