解:$(2)$设$∠BAG = x。$
∵$AE\perp AB,$
∴$∠EAG = 90°-∠BAG = 90°-x。$
∵$AG $平分$∠EAM,$
∴$∠EAM = 2∠EAG = 180°-2x,$
∴$∠BAM = 90°-∠EAM = 2x - 90°。$
∵$MN// PQ,$$AB// CD,$
∴$∠ABQ=∠BAM,$$∠CDQ=∠ABQ,$
∴$∠CDQ=∠BAM = 2x - 90°。$
∵$CD\perp DF,$
∴$∠FDQ = 90°+∠CDQ = 2x,$
∴$2∠BAG=∠FDQ。$
$ (3)∠HBD+∠AHB+∠BAH = 240°$或
$∠AHB+∠BAH-∠HBD = 120°。$
理由如下:
如图①,当点$H$在点$K$上方时,过点$H$
作$HT// MN,$则$HT// MN// PQ,$
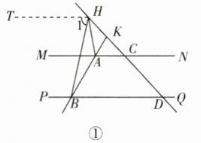
∴$∠1=∠HBD,$$∠MAB=∠ABD = 60°,$
$∠AHT+∠HAM = 180°,$
∴$∠HBD+∠AHB+∠HAM = 180°,$
∴$∠HBD+∠AHB+∠HAM+∠MAB = 240°,$
即$∠HBD+∠AHB+∠BAH = 240°;$
如图②,当点$H$在点$C,$$K$之间时,过点$H$作
$HT// MN,$则$HT// MN// PQ,$
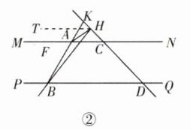
∴$∠HBD=∠THB,$$∠THA=∠HAC,$
$∠BAC = 180°-∠ABD = 120°,$
∴$∠HBD=∠THA+∠AHB=∠AHB+∠HAC$
∴$∠HBD=∠AHB+∠BAH-∠BAC,$
∴$∠AHB+∠BAH-∠HBD=∠BAC,$
即$∠AHB+∠BAH-∠HBD = 120°;$
如图③,当点$H$在点$C,$$D$之间时,过点$H$作
$HT// MN,$则$HT// MN// PQ,$
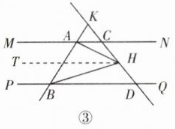
∴$∠HAN=∠AHT,$$∠BHT=∠HBD,$
$∠BAC = 180°-∠ABD = 120°,$
∴$∠AHT = 120°-∠BAH,$
∴$∠AHB=∠AHT+∠BHT $
$= 120°-∠BAH+∠HBD,$
∴$∠AHB+∠BAH-∠HBD = 120°。$
当点$H$在点$K$或点$C$处时,经检验,符合
$∠AHB+∠BAH-∠HBD = 120°。$
综上所述,满足条件的关系是
$∠HBD+∠AHB+∠BAH = 240°$或
$∠AHB+∠BAH-∠HBD = 120°。$